PCA Intro

PCA Intro#

Given \( X \in R^{n \times p}\), where we have \(n\) datapoints and \(p\) features, we would like to consider the first \(k\) directions in the high-dimensional feature space where most data lie on.

\(PC_1\) being the most important direction (captures the maximum variance in the data)

Each \(PC \in R^p\) is a linear combination of the original \(p\) features, scaled to unit norm

i.e. if \(PC_1 = (0.9, 0.1, 0)\), this means first feature (say x-axis) is most important, data are spreaded along x-axis, but don’t vary along y and z-axis)

Two ways to do PCA:

Eigendecomposition#

First is to obtain the eigen decomposition of the normalized gram matrix \(G \in R^{p \times p}\)

\[ G = \frac{1}{n-1}X^TX \]
\[ Gv_i = \lambda_i v_i \]

Each \(v_i \in R^{p}\) is a PC, or a direction in the feature space.

We obtain \(V = (v_1 \dots v_p) \in R^{p \times p}\) the eigenvector matrix, and \(\lambda = \text{diag}( \lambda_1 \dots \lambda_p)\) the eigenvalue matrix

\[ X^TXV = \lambda V \]

Second way is to do SVD

SVD#

\[ X = USV^T \]

Where \(U \in R^{n \times p}\), and \(S, V \in R^{p \times p}\).
Here \( S = \text{diag}( s_1 \dots s_p)\) is such that each \(s_i = \sqrt{\lambda_i}\), and \(V\) is still the PC matrix

We can project X onto PC and obtain \(X^{'} = XV \; \in R^{n \times p}\)

Note by orthogonality of \(V\), we have

\[ XV = USV^TV = US \]

So the \(j\) th col of \(US\) gives us the projected \(X\), or the coordinates on the \(j\) th PC, or \(V_j\)

We can also project \(X\) onto only the first \(k\) columns of \(V\), and obtain an \(n \times k\) matrix

\[ X^{'}_k = XV[:k] = USV^T(v_1 \dots v_k) = (U_1 s_1 \dots U_k s_k) \]

or the first \(k\) columns of \(U\), each multiplied by the singluar value \(s_i\)

We can reconstruct \(X\) from \(X^{'}_k \in R^{n \times k}\) by projecting it on \(V_k = (v_1 \dots v_k)^T \in R^{k \times p}\)

\[ \hat{X} = X^{'}_k (v_1 \dots v_k)^T \in R^{n \times p} \]

and when \(k = p\), we obtain the original \(X\)

Terminologies#

  • \(V\) is the principal components, with \(i\)-th col being \(PC_i\)

  • \(US = \sqrt{\lambda_i}U_i\) are refered to as the projections / principal coordinates / scores

  • \(VS = \sqrt{\lambda_i}V_i\) are the factor loadings, with each column being \(PC_i\) weighted by \(\sqrt{\lambda_i}\)

An Trivial Example#

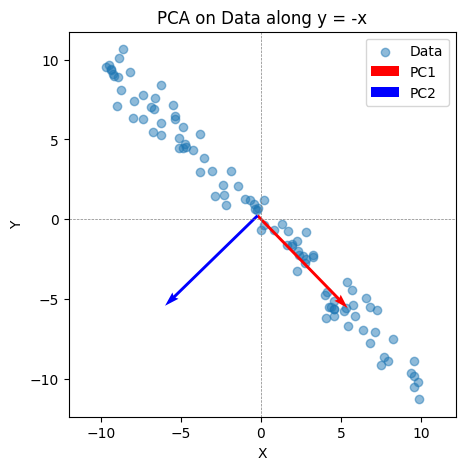
Consider trivial example in 2-dim, when we have data lying along the line \( y = -x\) plus some noise

We have \(X \in R^{n \times 2}\), with two features given by direction \((1, 0)\) and \((0, 1)\).

One would expect PC1 to give the direction \((1, -1)\).

Note the PC vector needs to have unit norm, giving roughly \((-0.7, -0.7)\)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# Step 1: Simulate data along the line y = -x
n = 100  # Number of points
x = np.random.uniform(-10, 10, n)  # Random x values
y = -x + np.random.normal(0, 1, n)  # y = -x + noise

X = np.column_stack((x, y))  # Shape (n,2)

# Step 2: Perform PCA
pca = PCA(n_components=2)
pca.fit(X)

# Principal components
pc1 = pca.components_[0]  # First principal component
pc2 = pca.components_[1]  # Second principal component

print("First principal component:", pc1)
print("Second principal component:", pc2)

# Mean of data
mean = np.mean(X, axis=0)

# Step 3: Visualize the data and principal components
plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], label="Data", alpha=0.5)

# Plot PC1 and PC2
plt.quiver(mean[0], mean[1], pc1[0], pc1[1], 
            color='r', scale=3, label="PC1")
plt.quiver(mean[0], mean[1], pc2[0], pc2[1], 
            color='b', scale=3, label="PC2")

plt.axhline(0, color='gray', linestyle='--', linewidth=0.5)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.5)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("PCA on Data along y = -x")
plt.legend()
plt.axis("equal")
plt.show()

First principal component: [ 0.6978726  -0.71622192]
Second principal component: [-0.71622192 -0.6978726 ]
../_images/f7dc7bce076f9588f0add542035bf95516b7671bbca9aa01aaa264a90edcbd23.png
Contents