Variational auto-encoder#
Intro#
The variational auto-encoder has one major difference with other stochastic simulation methods, in that it is interested not only in evaluating expectation of some intractable posterior, but also its gradient
Classical MC deals with \(\mathbb{E}_{p}[f(X)]\), where \(X \sim p_{\theta}(x)\), by drawing samples \(X_i\) from \(p\).
Now say we are interested in computing the gradient w.r.t. \(\theta\).
The unbiased MC estimator is given by
Which we can compute by simulating \(X_i \sim p(x)\), assuming we can compute \( \nabla_\theta \log p(x) \):
This is also known as the score function estimator
Reparameterization trick#
The unbiased estimator has large variance. Usually as long as \(f(x)\) is differentiable, we can use the trick:
Consider \( x = g_{\theta}(\epsilon) \), where \(\epsilon \sim p(\epsilon)\) is some auxiliary variable with no parameter of interest.
We usually deal with the gaussian case \( X \sim \mathbb{N}(\mu_{\theta}, \Sigma_{\theta}) \), so we write \( X = \mu_{\theta} + \sigma_{\theta} \epsilon \),
where \( \epsilon \sim \mathbb{N}(0, I) \), \( \sigma_{\theta} \sigma_{\theta}^T = \Sigma\), and \( \mu_{\theta}, \sigma_{\theta} \) are deterministic functions parametrized by \(\theta\).
Where \(\Sigma\) is not diagonal, we can find \( \sigma_{\theta} \) with Chelosky
Then we init \(\mu_{\theta}, \sigma_{\theta}\) and simulate \(\epsilon^{(j)}\), compute \( X^{(j)} = \mu_{\theta} + \sigma_{\theta} \cdot \epsilon^{(j)} \), so that
and
So that all we have to do is to simulate \(\epsilon \sim p(\epsilon)\), compute MC estimate of \(f(\mu_{\theta} + \sigma_{\theta} \cdot \epsilon^{(j)})\), then differentiate it
Bayesian Setup for VAE#
Now consider \(E_q [ p(x | z) ] \), where \( z \sim q_{\phi}(z | x) \), and \( x \sim p_{\theta}(x | z) \)
With the usual setup \(z \in \mathbb{R}^d\) is latent, and \(d\) is the latent_dim.
Let posterior \( q_{\phi}(z | x) = \mathbb{N}(\mu_{\phi}(x), \sigma_{\phi}(x))\)
The likelihood \( p(x | z)\) is either gaussian or Bernoulli (for binary image, where each pixel is 0 or 1). In this case let \( p_{\theta}(x | z) = \mathbb{N}(\mu_{\theta}(z), \sigma_{\theta}(z))\)
As we with to learn the best \(p_{\theta}\) and \(q_{\phi}\) given the data \(x\), we wish to compute \( \nabla_\theta E_q [ p(x | z) ]\) and \( \nabla_\phi E_q [ p(x | z) ]\), which will be used to update \(\mu_{\theta}, \sigma_{\theta}, \mu_{\phi}, \sigma_{\phi}\).
In fact in the VAE case, \(p_{\theta}\) is a neural net named Decoder, which takes \(z\) as input, and outputs the tuple \( ( \mu_{\theta}(z), \sigma_{\theta}(z) )\),
with \(\theta\) be its parameters which we will perform SGD.
Similarly \(q_{\phi}\) is the Encoder neural net which takes \(x\) and outputs a distribution for \(z\), given by \(\mu_{\phi}, \sigma_{\phi}\) and parametrized by \(\phi\)
Given data \(x\), we evaluate \( \nabla_{(\theta, \phi)} E_q [ p(x | z) ]\)
The unbiased score-based estimator is
By simulating \(z^{(j)} = \mu_{\phi}(x) + \sigma_{\phi}(x) \cdot \epsilon^{(j)} \), we can do
ELBO#
Deriving ELBO#
Consider the log marginal likelihood
By Jensen’s inequality we have
This is the ELBO (a lower bound of the log likelihood, often a negative number). The negative ELBO is given by
Where the first term is the recon loss (negative log likelihood loss), and the second term is the KL loss. We want to minimize recon loss (maximizing likelihood under our best posterior \(q(z|x)\)), while keeping \(q(z|x)\) not too far from prior
Note that
This means that as we maximize ELBO towards its upper bound \( \log p_\theta(x) \), we are minimizing \(D_{KL}(q_\phi(z \mid x) \| p_\theta(z \mid x)) \) at the same time, hence making our posterior converge to the true posterior \( p_\theta(z \mid x) \)
Computing ELBO Loss#
We know -ELBO = Recon_loss + KL
Denote ELBO as \(\mathcal{L}(\theta, \phi; x)\), we have
The unbiased MC estimator (SGVB) is given by sampling \(z^{(j)} = \mu_{\phi}(x) + \sigma_{\phi}(x) \cdot \epsilon^{(j)} \)
Then the gradient \( \nabla_{(\theta, \phi)} \hat{\mathcal{L}}\) is evaluated on a mini-batch \(\{X_i\}_{i \in \mathbb{D}_m}\).
Since we are using the reparametrization, this estimator has very low variance, and we can even set \(L = 1\)
So that with each batch of data \(x\) (64, 28, 28), we only sample (64,) \(\epsilon\) to obtain \(\hat{z} \sim \mathbb{N}(\mu_z, \sigma_z^2) = q(z \mid x) \),
\(\hat{z}\) is fed into decoder to obtain \( \mu_x, \sigma_x \), where \( p(x \mid z) = \mathbb{N}(\mu_x, \sigma_x^2) \)
We can then evaluate the recon loss as \( - \log p(x \mid \hat{z}) \) as the one-sample MC estimate of \( E_q [- \log p(x \mid z)] \)
The full MC algo is given by
Init \( \phi, \theta, L \)
Sample minibatch of data \(x\) (64, 28, 28)
Obtain \( q_\phi(z \mid x) = N(\mu_z, \Sigma) \) with encoder(x)
Sample \(\epsilon_{ij}\) for each \(x_i\) in batch, \(j = 1, ..., L\), shape \((64, L)\)
Obtain \(\hat{z}_{ij} \sim q(z \mid x) = \mu_z + \Sigma \cdot \epsilon\)
Obtain batch MC estimate for recon loss: \( - \frac{1}{L} \sum \log p(x \mid z^{(j)}) \)
Obtain batch MC estimate for KL div: \( - \frac{1}{L} \sum \log \frac{p(z^{(j)})}{\left( q_\phi(z^{(j)} \mid x) \right)} \)
Compute batch grad \( \frac{1}{M} \sum_{x_i \in \mathbb{D}_m} \nabla_{(\theta, \phi)} \hat{\mathcal{L}}^L\)
Update SGD on \( \theta, \phi \)
Recon Loss#
Like above, we showed that by simulating \(z^{(j)} = \mu_{\phi}(x) + \sigma_{\phi}(x) \cdot \epsilon^{(j)} \)
and
We can pick \(N = 1\), which has been shown to work well empirically. Even if some data generates noisy estimate of the grad, averaging over a mini-batch often smoothes it out
When implementing, we do not need to manually implement the grad taking step, but we only need to make the encoder(\(\phi\)) and decoder(\(\theta\)) differentiable, and outputs the MC estimate for the loss $\( -E_{q}[ \log p(x | z) ] \approx -\log p(x | z^{(j)}) \)$
Then we simply call autograd and optimizer to compute the grad and perform SGD
loss.backward()
gradients = [v.value.grad for v in self.trainable_weights]
with torch.no_grad():
optimizer.apply(gradients, self.trainable_weights)
import os
os.environ['KERAS_BACKEND'] = 'torch'
import keras
from keras import ops
def compute_nll(self, data):
z_mean, z_log_var = self.encoder(data)
epsilon = keras.random.normal(ops.shape(z_mean))
z_std = ops.exp(0.5 * z_log_var)
z_sample = z_mean + (z_std * epsilon)
x_mean, x_log_std = self.decoder(z_sample)
log_Z = 0.5 * ops.log(2 * self.pi)
nll_loss = 0.5 * ops.square((data - x_mean) / ops.exp(x_log_std)) + x_log_std + log_Z
nll_loss = ops.mean(ops.sum(nll_loss, axis=[-1, -2]))
KL Div#
To compute KL Div, while one could do MC estimate of KL after sampling \(z^{(j)}\):
In our case when \( q(z \mid x) \) and prior \( p(z) \) are both gaussian, KL can be computed analytically (as soon as we have \( q(z \mid x) \) using the encoder)
Let
Where \(\mu \in R^d \) is output of \(\mu_\phi(x)\), and \(\Sigma = \text{diag}(\sigma_1^2 \dots \sigma^2_d)\) is output of \(\sigma_\phi(x)\), where \(d\) is the latent_dim, often set to 2.
Then we have
So that
We have that under \(z \sim q(z|x)\):
So that
This is then averaged across the mini-batch for computation of the batch gradient:
def compute_kl(self, data):
z_mean, z_log_var = self.encoder(data)
kl_loss = 0.5 * ops.sum((ops.square(z_mean) + ops.exp(z_log_var) - 1 - z_log_var), axis=-1)
kl_loss = ops.mean(kl_loss)
Full Algorithm#
Now being able to compute KL analytically, we do
Init
Encoderwith params \( \phi\), decoder with \(\theta\), set \(L=1\)Sample minibatch of data \(x\) (64, 28, 28)
Forward pass
Encoder\(f_{\phi}(x)\) = \((\mu_z, \log \Sigma)\), each (64, 2)Obtain \( q_\phi(z \mid x) = N(\mu_z, \Sigma) \)
Use \( q_\phi(z \mid x) \) to compute KL div analytically
Obtain \(\sigma_z = \exp(0.5 \log \Sigma)\)
Simulate \(\hat{z}_{j} \sim q(z \mid x) = \mu_z + \sigma_z \cdot \epsilon\)
Forward pass
Decoder\(f_{\theta}(\hat{z}_{j})\) = \((\mu_x, \Sigma_x)\)Obtain \( p(x \mid z^{(j)}) = N(\mu_x, \Sigma_x) \)
Plug in \(\hat{z}_{j}\) for recon loss: \( - \log p(x \mid z^{(j)}) \)
output loss = KL div + recon loss to autograd
SGD with
EncoderandDecoder
Full VAE setup on MNIST#
The full setup on MNIST, using torch backend and Keras API:
Preprocessing#
from keras.datasets import mnist
(x_train, y_train), (x_val, y_val) = mnist.load_data()
type(x_train), x_train.shape, y_train.shape
(numpy.ndarray, (60000, 28, 28), (60000,))
from torch.utils.data import TensorDataset, DataLoader
def preprocess(image, label):
return ops.cast(image, 'float32') / 255., ops.one_hot(label, 10)
x_train, y_train = preprocess(x_train, y_train)
x_val, y_val = preprocess(x_val, y_val)
train_ds = TensorDataset(x_train, y_train)
val_ds = TensorDataset(x_val, y_val)
train_loader = DataLoader(train_ds, batch_size=64, shuffle=True)
val_loader = DataLoader(val_ds, batch_size=64)
Encoder#
The encoder \(f_{\phi}(x)\) takes a batch of images, (64, 28, 28), and returns \(\mu_z\) and \(\log \sigma^2_z\),
where \( q(z \mid x) = \mathbb{N}(\mu_z, \text{Diag}(\sigma^2_z)) \)
\(\mu_z\) and \(\log \sigma^2_z\) are of shape (64, 2), where 2 is latent dim
from keras.models import Model
from keras.layers import Input, Dense, Flatten
latent_dim = 2
image_shape = (28, 28)
image_input = Input(shape=image_shape, name='image')
x = Flatten()(image_input)
x = Dense(512, activation='relu')(x)
x = Dense(512, activation='relu')(x)
x = Dense(2 * latent_dim)(x)
z_mean, z_log_var = ops.split(x, 2, axis=-1)
encoder = Model(inputs=image_input, outputs=[z_mean, z_log_var], name='encoder')
z_mean, z_log_var = encoder([keras.random.normal((64, 28, 28))])
z_mean.shape, z_log_var.shape
/home/jx1421/DL_TensorFlow_Imperial/DL_venv/lib64/python3.9/site-packages/keras/src/models/functional.py:237: UserWarning: The structure of `inputs` doesn't match the expected structure.
Expected: image
Received: inputs=['Tensor(shape=torch.Size([64, 28, 28]))']
warnings.warn(msg)
(torch.Size([64, 2]), torch.Size([64, 2]))
Decoder#
The decoder \(f_\theta(z)\) takes a batch of \(\hat{z} = \mu_z + \sigma_z \cdot \epsilon \sim q(z \mid x)\), (64, 2)
and returns the mean of the reconstructed image \(\mu_x\) (64, 28, 28)
where we assumed \(\sigma^2_x=0.5\), s.t. \( p(x \mid z) = \mathbb{N}(\mu_x, \text{Diag}(0.5)) \)
from keras.layers import Reshape
z_input = Input(shape=(latent_dim,), name='z')
x = Dense(512, activation='relu')(z_input)
x = Dense(512, activation='relu')(x)
x = Dense(28 * 28)(x)
x = Reshape((28, 28))(x)
decoded_image = ops.sigmoid(x)
decoder = Model(inputs=z_input, outputs=decoded_image, name='decoder')
decoder.summary()
Model: "decoder"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ z (InputLayer) │ (None, 2) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_3 (Dense) │ (None, 512) │ 1,536 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_4 (Dense) │ (None, 512) │ 262,656 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_5 (Dense) │ (None, 784) │ 402,192 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ reshape (Reshape) │ (None, 28, 28) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ sigmoid (Sigmoid) │ (None, 28, 28) │ 0 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 666,384 (2.54 MB)
Trainable params: 666,384 (2.54 MB)
Non-trainable params: 0 (0.00 B)
VAE#
from keras.metrics import Mean
import torch
import numpy as np
class VAE(Model):
def __init__(self, encoder, decoder, num_mc_samples=1, **kwargs):
super().__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.loss_metric = Mean(name='loss')
self.nll_metric = Mean(name='nll')
self.kl_metric = Mean(name='kl')
self.pi = ops.array(np.pi)
self.L = num_mc_samples
def compute_losses(self, data):
z_mean, z_log_var = self.encoder(data[0])
kl_loss = (0.5 * ops.sum((ops.square(z_mean)
+ ops.exp(z_log_var) - 1 - z_log_var), axis=-1))
kl_loss = ops.mean(kl_loss)
epsilon = keras.random.normal(ops.shape(z_mean))
z_std = ops.exp(0.5 * z_log_var)
z_sample = z_mean + (z_std * epsilon)
x_mean = self.decoder(z_sample)
log_Z = 0.5 * ops.log(2 * self.pi)
# recon loss, or p(x|z) = N(x|mu, 0.5)
nll_loss = (0.5 * ops.square((data[0] - x_mean)
/ 0.5) + ops.log(0.5) + log_Z)
nll_loss = ops.mean(ops.sum(nll_loss, axis=[-1, -2]))
loss = kl_loss + nll_loss
return loss, kl_loss, nll_loss
def call(self, inputs):
z_mean, z_log_var = self.encoder(inputs)
epsilon = keras.random.normal(ops.shape(z_mean))
z_std = ops.exp(0.5 * z_log_var)
z_sample = z_mean + (z_std * epsilon)
return self.decoder(z_sample)
def train_step(self, data):
assert keras.config.backend() == 'torch'
self.zero_grad()
loss, kl_loss, nll_loss = self.compute_losses(data)
loss = ops.mean(loss)
loss.backward()
gradients = [v.value.grad for v in self.trainable_weights]
with torch.no_grad():
self.optimizer.apply(gradients, self.trainable_weights)
self.loss_metric.update_state(loss)
self.nll_metric.update_state(nll_loss)
self.kl_metric.update_state(kl_loss)
return {m.name: m.result() for m in self.metrics}
def test_step(self, data):
loss, kl_loss, nll_loss = self.compute_losses(data)
loss = ops.mean(loss)
self.loss_metric.update_state(loss)
self.nll_metric.update_state(nll_loss)
self.kl_metric.update_state(kl_loss)
return {m.name: m.result() for m in self.metrics}
@property
def metrics(self):
return [self.loss_metric, self.nll_metric, self.kl_metric]
vae = VAE(encoder, decoder)
from keras.callbacks import EarlyStopping
early_stop = EarlyStopping(patience=10)
vae.compile(optimizer="adam")
# Manually call the model with a batch of data to build it
for batch in train_loader:
vae(batch[0])
break
history = vae.fit(train_loader, validation_data=val_loader,
epochs=20, callbacks=[early_stop])
Epoch 1/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 4.4977 - loss: 280.1234 - nll: 275.6256 - val_kl: 4.6310 - val_loss: 254.6410 - val_nll: 250.0101
Epoch 2/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 4.8191 - loss: 252.8121 - nll: 247.9931 - val_kl: 5.3388 - val_loss: 248.5372 - val_nll: 243.1984
Epoch 3/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 5.3350 - loss: 248.1796 - nll: 242.8446 - val_kl: 5.4204 - val_loss: 246.6304 - val_nll: 241.2100
Epoch 4/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 5.5311 - loss: 246.1467 - nll: 240.6157 - val_kl: 5.4211 - val_loss: 245.3051 - val_nll: 239.8839
Epoch 5/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 5.6911 - loss: 244.7868 - nll: 239.0956 - val_kl: 5.8418 - val_loss: 244.1463 - val_nll: 238.3045
Epoch 6/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 10s 11ms/step - kl: 5.8211 - loss: 243.5906 - nll: 237.7696 - val_kl: 5.6949 - val_loss: 243.4613 - val_nll: 237.7663
Epoch 7/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 5.8978 - loss: 242.7922 - nll: 236.8943 - val_kl: 5.9343 - val_loss: 242.9776 - val_nll: 237.0433
Epoch 8/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 12s 12ms/step - kl: 5.9751 - loss: 242.3112 - nll: 236.3362 - val_kl: 5.8855 - val_loss: 242.2815 - val_nll: 236.3960
Epoch 9/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 6.0407 - loss: 241.7035 - nll: 235.6628 - val_kl: 5.9695 - val_loss: 242.0277 - val_nll: 236.0583
Epoch 10/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 6.0942 - loss: 241.1679 - nll: 235.0737 - val_kl: 5.9323 - val_loss: 241.7631 - val_nll: 235.8309
Epoch 11/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 6.1474 - loss: 240.8526 - nll: 234.7052 - val_kl: 6.0986 - val_loss: 241.5895 - val_nll: 235.4910
Epoch 12/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.1604 - loss: 240.7273 - nll: 234.5668 - val_kl: 6.1131 - val_loss: 240.9781 - val_nll: 234.8651
Epoch 13/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.2039 - loss: 240.1791 - nll: 233.9753 - val_kl: 6.1311 - val_loss: 240.9396 - val_nll: 234.8085
Epoch 14/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.2482 - loss: 240.0677 - nll: 233.8195 - val_kl: 6.1193 - val_loss: 241.0337 - val_nll: 234.9145
Epoch 15/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.2299 - loss: 239.9848 - nll: 233.7548 - val_kl: 6.2474 - val_loss: 240.5508 - val_nll: 234.3034
Epoch 16/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 6.2935 - loss: 239.5424 - nll: 233.2489 - val_kl: 6.1843 - val_loss: 240.1398 - val_nll: 233.9556
Epoch 17/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.3047 - loss: 239.2993 - nll: 232.9946 - val_kl: 6.2655 - val_loss: 240.0608 - val_nll: 233.7953
Epoch 18/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.3255 - loss: 239.1584 - nll: 232.8329 - val_kl: 6.1793 - val_loss: 239.9045 - val_nll: 233.7253
Epoch 19/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 11ms/step - kl: 6.3572 - loss: 239.0670 - nll: 232.7097 - val_kl: 6.3855 - val_loss: 240.0855 - val_nll: 233.7000
Epoch 20/20
938/938 ━━━━━━━━━━━━━━━━━━━━ 11s 12ms/step - kl: 6.3756 - loss: 238.8625 - nll: 232.4868 - val_kl: 6.3244 - val_loss: 239.6615 - val_nll: 233.3372
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(15, 4))
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='val')
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Loss vs epoch")
plt.legend()
<matplotlib.legend.Legend at 0x7fb3315b77c0>
vae.evaluate(val_loader, return_dict=True)
1/157 ━━━━━━━━━━━━━━━━━━━━ 2s 13ms/step - kl: 6.3114 - loss: 236.7239 - nll: 230.4125
157/157 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - kl: 6.2407 - loss: 240.2854 - nll: 234.0447
{'kl': 6.324409008026123, 'loss': 239.7041473388672, 'nll': 233.37974548339844}
Visualization#
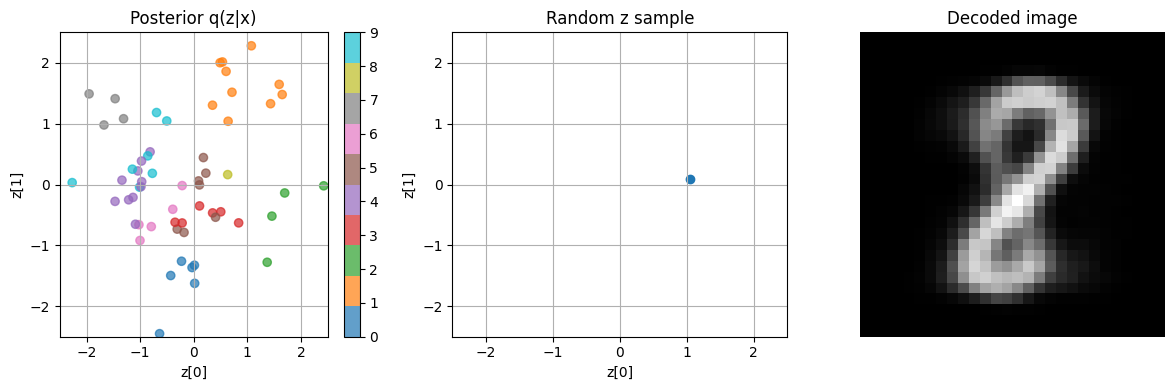
To visualize VAE, we simply generate random \(\hat{z}\) in the latent space.
Note the idea of VAE is that given an image \(x\), if we can obtain the right posterior \(q(z \mid x)\) (thru training the encoder), then passing a sample \(\hat{z} \sim q(z \mid x) \) into the decoder should yield a \(x_{recon}\) sufficiently close to \(x\)
We can visualize the learnt posterior \(q(z|x=x_{val})\), and generate some \(z \sim \mathbb{N}(0, I)\), and inspect which \(x_{val}\) most likely generated this \(z\).
Then we can obtain \(x_{recon}\) with the decoder, and inspect if it agrees with \(x_{val}\)
# visualize the posterior q(z|x) for a batch of data
for batch in val_loader:
images, labels = batch
z_mean, z_log_var = vae.encoder(images)
break
# convert one-hot labels to class indices
labels = torch.argmax(labels, dim=1).cpu().numpy()
z_mean = z_mean.cpu().detach().numpy()
fig, axs = plt.subplots(1, 3, figsize=(12, 4))
# subplot 1: plot Posterior q(z|x)
sc = axs[0].scatter(z_mean[:, 0], z_mean[:, 1], c=labels, cmap='tab10', alpha=0.7)
axs[0].set_title("Posterior q(z|x)")
axs[0].set_xlabel("z[0]")
axs[0].set_ylabel("z[1]")
axs[0].set_xlim(-2.5, 2.5)
axs[0].set_ylim(-2.5, 2.5)
axs[0].grid(True)
# Add colorbar to subplot 1
cbar = fig.colorbar(sc, ax=axs[0], ticks=range(10))
# generate one random z ~ N(0, I)
z_random = keras.random.normal((1, latent_dim))
z_rand_np = z_random.cpu().detach().numpy() # for plotting
decoded_images = vae.decoder(z_random)
decoded_images = ops.convert_to_numpy(decoded_images)
print('decoded image shape:', decoded_images.shape)
# Subplot 2: Random latent z (inspect where z is in q(z|x) space)
axs[1].scatter(z_rand_np[:, 0], z_rand_np[:, 1])
axs[1].set_title("Random z sample")
axs[1].set_xlabel("z[0]")
axs[1].set_ylabel("z[1]")
axs[1].set_xlim(-2.5, 2.5)
axs[1].set_ylim(-2.5, 2.5)
axs[1].grid(True)
# Subplot 3: Decoded image
axs[2].imshow(decoded_images[0], cmap='gray')
axs[2].set_title("Decoded image")
axs[2].axis('off')
plt.tight_layout()
plt.show()
decoded image shape: (1, 28, 28)
# generate 9 random z ~ N(0, I)
z_random = keras.random.normal((9, latent_dim))
decoded_images = ops.convert_to_numpy(vae.decoder(z_random))
n_rows, n_cols = 3, 3
fig, axes = plt.subplots(n_rows, n_cols, figsize=(9, 8))
fig.subplots_adjust(hspace=0., wspace=0.)
for n, image in enumerate(decoded_images):
row = n // n_cols
col = n % n_cols
axes[row, col].imshow(image, cmap='gray')
axes[row, col].get_xaxis().set_visible(False)
axes[row, col].get_yaxis().set_visible(False)
plt.show()
