Greeks

Greeks#

Option pricing#

Option pricing is related to the greeks via Taylor expansion:

\[ \Delta V \approx \Delta \cdot \Delta S + \Theta \cdot \Delta t + \text{Vega} \cdot \Delta \sigma + \frac{1}{2} \Gamma \cdot (\Delta S)^2 \]

Long an option gives you exposure to delta, theta, vega, and second-order exposure to Gamma (ignoring other 2nd-order greeks for now)

Delta#

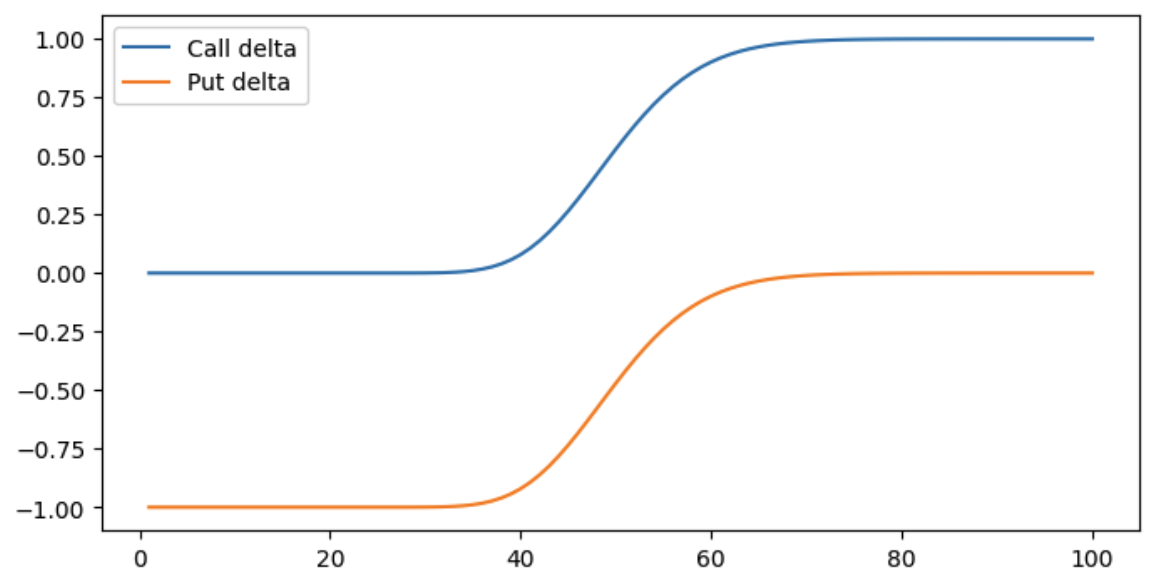
For shorted-dated option, ATM call and put should roughly have \( \Delta = \pm 0.5 \). This is because we have for ATM call (\(S = K\)), as \( T \to 0\):

\[ d_{1,2} = \frac{\left(r \pm \frac{\sigma^2}{2}\right)T}{\sigma \sqrt{T}} \to \frac{\sigma \sqrt{T}}{2} \to 0 \]
\[ \phi(d_1), \phi(d_2) \to 0.5 \]

For long-dated option, all have delta around 0.5 (ITM delta slighly larger than OTM)

See from the image, where x-axis is \(S\). For a call and put option with same \(K\) and \(T\), as price up, call delta converges to 1, while put becomes OTM and delta converges to 0. vice versa

Alt Text

Gamma#

Gamma \( \Gamma\) is sensitivity of Delta to price \( \frac{\partial \Delta}{\partial S} \), or equivalently the convexity of the option price (as a function of underlying \( S\) )

For all options we have \( \Gamma > 0\)

Trading Gamma while hedging delta is essentially a bet on Realized Vol.

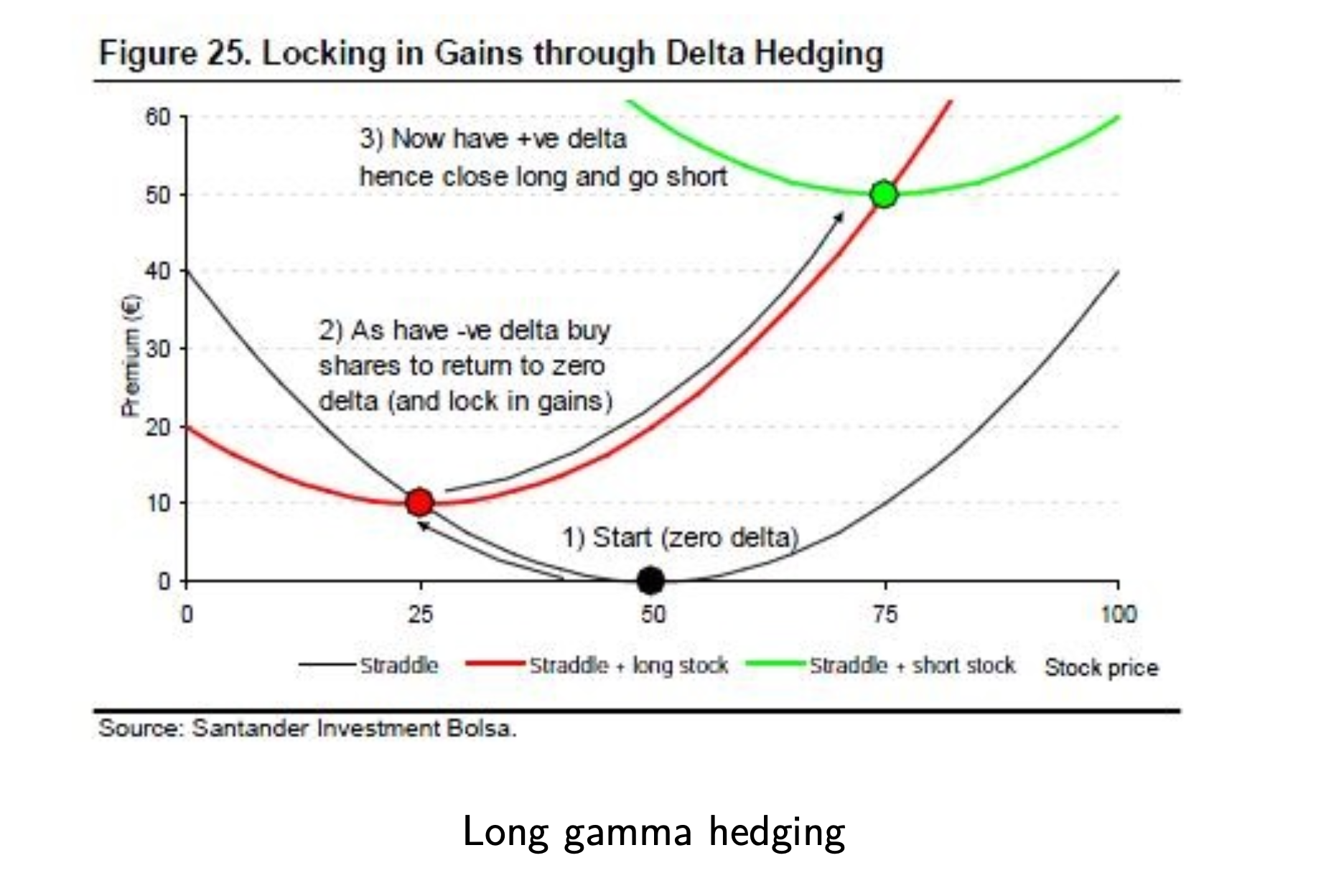
If one identifies high gamma (convex trade), can start with long straddle (buy call + put) with flat delta. If prive moves up, drives up delta (\( \Gamma > 0 \) means \(\Delta\) up when \(S\) up), we can sell stock at the higher price to hedge delta, and hence profit. Convexity means call option prive moves up faster than linear rate, at which prive moves up.

Similarly put option moves up faster than rate at which price drops. If prive moves down, our delta becomes negative, so long stock at low point to hedge the delta, meanwhile profit.

If price doesn’t move as much (low realized Vol), we lose the initial premium.

Note ATM has highest Gamma. An ATM call option (with \(\Delta=0.5\)) quickly becomes ITM (hence larger delta) if price increases, or becomes OTM and much smaller delta if price decreases. Note this is more true when \(T\) is small (near expiry).

When \(T\) is far-dated, all options have small Gamma, as price changes now don’t really impact an option expiring in the long future.

Alt Text

Vega#

Vega is WRT change in implied vol (always > 0 for options)

Note we cannot compute IV analytically, have to numerical (bisection or newton)

For far-dated option, vega drives the option price more than \(\Gamma\). Usually changes in RV drives IV too, (i.e. long straddle is long vega and long gamma, profit from stock price moving)

But one can also long vega in far-dated option which has low Gamma. For example, IV gets high before key announcements (as investors buy options to bet on the stock performance), and one can sell IV to earn the premium by shorting options.

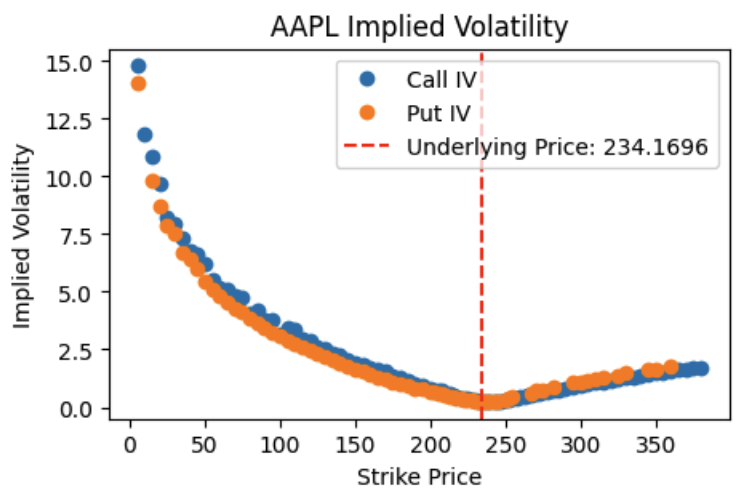
  • OTM call options (high strike) have higher IV, as they are cheap and many retail investors want to bet on outsized return of key stocks (like Tesla/nvidia etc).

  • OTM put options (low strike) have higher IV, as institutions long stock need to buy OTM put for hedging / insurance.

When plotting IV w.r.t. strike, (where one uses IV(call) for \(K > S\) and IV(put) for \(K<S\)), one observes a smile, with lowest IV at \(K=S\), and higher IV both ways. This basically means there is higher demand for OTM calls and OTM puts, and people are willing to pay premium for them. A strategy (risky) is to short them, bear the tail risk and earn the premium.

Referencing my apple analysis for the vol smile

Alt Text

Contents