Simulating Black-Scholes with Monte Carlo

Simulating Black-Scholes with Monte Carlo#

Black Scholes#

\[ C = S_0 \Phi(d_1) - K e^{-rT} \Phi(d_2) \]
\[ d_1 = \frac{\ln\left(\frac{S_0}{K}\right) + \left(r + \frac{\sigma^2}{2}\right)T}{\sigma \sqrt{T}}, \quad d_2 = d_1 - \sigma \sqrt{T} \]

Assumptions:

  • Stock follows geometric Brownian motion.

  • Constant risk-free rate

  • No arbitrage.

  • No transaction costs.

  • European option

Geometric Brownian Motion#

\[dX_t=\mu X_tdt+\sigma X_tdW_t\]

where \(\mu\), \(\sigma\in\mathbb{R}\) and \(W_t-W_s\sim\mathcal{N}(0, t-s)\).

Discrete Approximation of Brownian Motion#

We will use a Euler discretisation for the simulation.

\[X_{t+1}=X_t+\mu X_t dt+\sigma X_tdW_t\]
\[ dW_t \sim N(0, dt) \]

Note $\( W_t = W_{t-1} + dW_t, \quad \text{where } dW_t \sim N(0, dt). \)\( or \)\( W_t = \sum_{i=1}^n dW_i, \)$

so $\( \text{Var}(W_t) = n \cdot dt \)$

In continuous-time process#

\[ \mathbb{E}[W_t^2] = \text{Var}(W_t) = T \]

This means if we set dt = 0.01, and simulate for n = 100 timestamps, this is equivalent to T = 1 year in Black-Scholes

Black-Scholes#

\[ d_1 = \frac{\ln(S / K) + (r + 0.5 \sigma^2) T}{\sigma \sqrt{T}} \]

For call: $\( \Delta = N(d1) \)$

For put: $\( \Delta = N(d1) - 1 \)$

Gamma: $\( \Gamma = \frac{\phi(d_1)}{S \sigma \sqrt{T}} \)$

from base import GBM, Option
import torch
import matplotlib.pyplot as plt

mu, sig = 0.02, 0.15
x0, strike = 1.0, 1.0
dt, T = 0.01, 1.0

call = Option(mu, sig, x0, strike, dt = 0.01, n_paths=100000, option_type='Call', device='cuda')
call.simulate()
call.compute_payoff()
print('price', call.price)
print('delta', call.compute_delta())

Simulation done
price 0.06985085465508467
delta 0.5951619148254395

call.black_scholes(print_=True)

price:  0.06961840391159058
Delta:  0.5825156569480896
Gamma:  2.6025195121765137

0.06961840391159058

call.plot()

Too many paths to plot. Plotting first 1000 paths
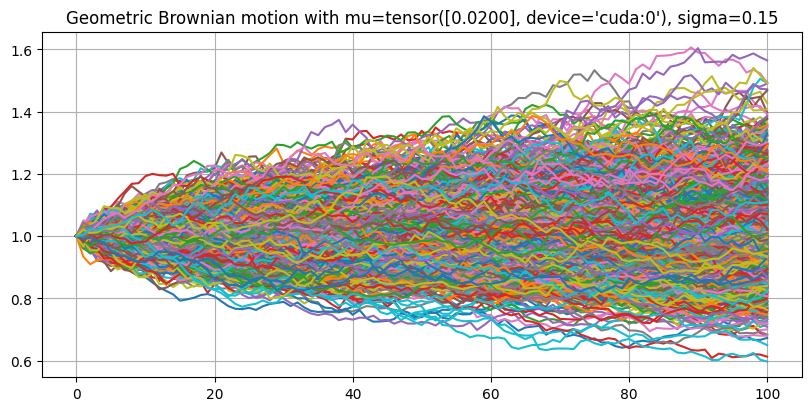
../_images/bfc9f826aaa295b0fb342c7e873df98e8b55680511181a897b8ef247ac49c373.png 
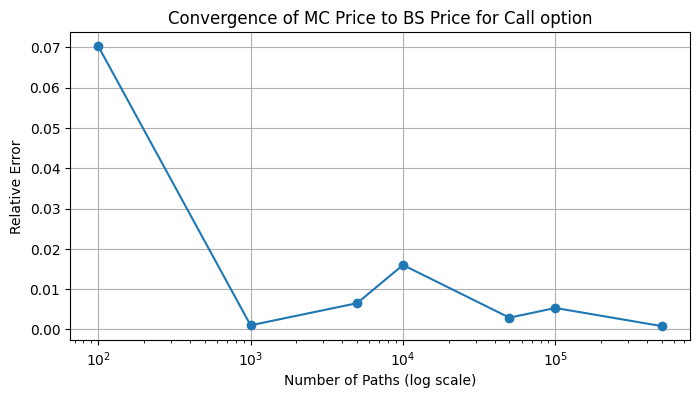
n_paths_values = [int(x) for x in [100, 1000, 5000, 10000, 50000, 1e5, 5e5]]
call.plot_accuracy(n_paths_values)

Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
../_images/0bb73f0146ed9f55658785470724d46cfdf51c77d6b3462ae6a05b4ed1ab0d6c.png 
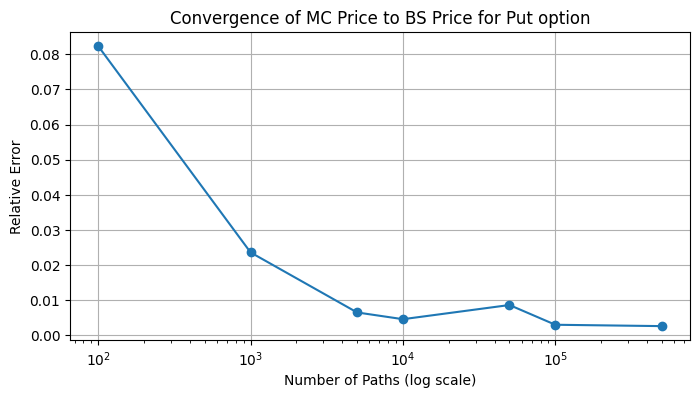
put = Option(mu, sig, x0, strike, dt = 0.01, n_paths=1000, option_type='Put', device='cuda')
put.plot_accuracy(n_paths_values)

Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
Simulation done
../_images/2aff3b3d196e2afafa669c91a55dc4c36721376b6f9252a8b3b3b6871a8da083.png 
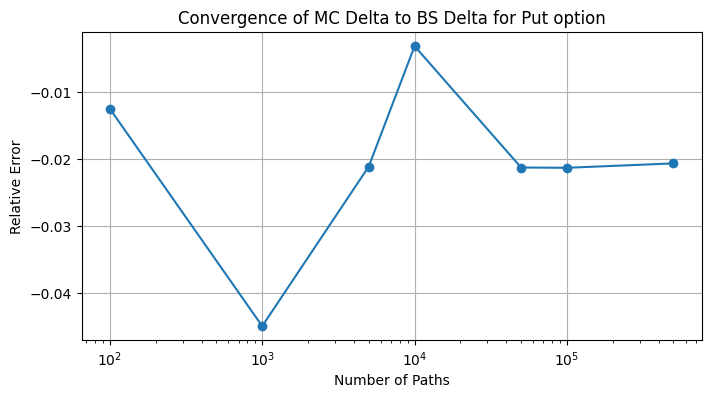
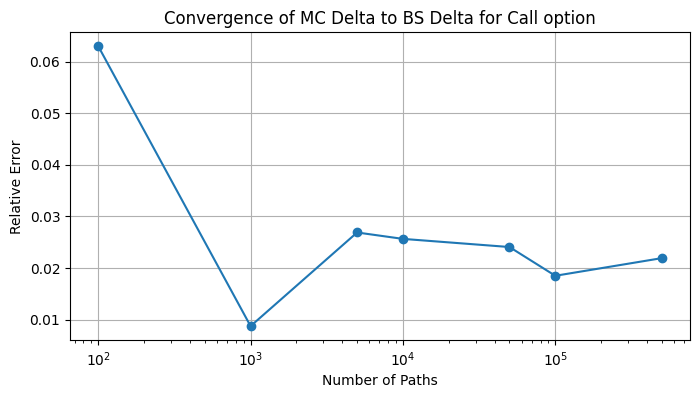
call.plot_delta(n_paths_values)

BS Delta:  0.5825156569480896
Simulation done
MC Delta:  0.6192039847373962
Simulation done
MC Delta:  0.5774345397949219
Simulation done
MC Delta:  0.5981668829917908
Simulation done
MC Delta:  0.597444474697113
Simulation done

MC Delta:  0.5965250134468079
Simulation done
MC Delta:  0.5932795405387878
Simulation done
MC Delta:  0.5952727794647217
../_images/ebfb5af27aefa732bf8876afc614b6980c2912104fb834e02dfc97b270072911.png 
put.plot_delta(n_paths_values)

BS Delta:  -0.4174843430519104
Simulation done
MC Delta:  -0.4226855933666229
Simulation done
MC Delta:  -0.4362458288669586
Simulation done
MC Delta:  -0.4262937903404236
Simulation done
MC Delta:  -0.41878122091293335
Simulation done
MC Delta:  -0.4263526201248169
Simulation done
MC Delta:  -0.4263691008090973
Simulation done
MC Delta:  -0.4260958731174469
../_images/a46d1a61ef1a4ea02368261dc9e0428c6ed5302a0b44fd153e97f12e33c4b664.png
Contents